Динамо-машины  Нелинейная электромеханика 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 [ 99 ] 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118

sect;6.5. Равновесие струны

будет

-1/2

{h - dxf 2

1 , h-l/2m\

Введя безразмерные величины получим уравнение равновесия

= liiol44/ch\

v = ap{v), p{v) = -( +-ln-

h + i/2m J

(6.4.7) (6.4.8)

(6.4.9)

При всех a это уравнение имеет решение v = О, отвечающее недеформированной системе. Остальные решения определяются из уравнения

1 1 l-t;\

I Ifi

1 - 2v l-\-v J

(6.4.10)

Соответствующая кривая равновесий представлена на рис. 6.10. Чтобы найти точку ветвления, нужно вычислить предел левой части (6.4.10) при v 0; это дает а = л/З/2. Касательная к ветви (6.4.10) при V = О вертикальна (рис. 6.10). Поэтому точка ветвления представляет собой одновременно предельную точку и точку бифуркации (скрещения). Учитывая, что ветвь г = О, лежащая между точкой а = О и точкой ветвления, устойчива, находим, что остальные ветви неустойчивы.

Как и в предыдущем примере, рассмотренная система может реально находиться в равновесии лишь при ограниченных значениях параметра. Однако теперь это связано не с Рис. 6.10 исчезновением решений (решение v = О существует нри всех а), но с потерей устойчивости.

sect; 6.5. Равновесие струны

иод действием магнита

и заданной внегнней нагрузки

Рассмотрим тонкую натянутую ферромагнитную струну, притягиваемую электромагнитом и загруженную равномерно распределенной нагрузкой q. Считаем, что магнитная проницаемость струны, магнита

Глава 6. Задачи нелинейной теории

и магнитопровода бесконечно велика, а линии индукции замыкаются, согласно рис. 6.2, и охватываются одним и тем же полным током /. Пусть b - ширина, I - длина струны, h - расстояние между недеформированной струной и магнитом, и{х) - перемеш,ения точек струны. Предполагается, что h b I и и сравнимо с А. Удерживая, в выражении для пондеромоторных сил младший член относительно и/Ь придем к краевой задаче

{1-V

+7 = 0,

г;= v{0)=v{a)=0,

2 Ро а =

2ГАЗ fiobP

Здесь V, г - безразмерные перемегцения и координата, Т - натяжение, /io - магнитная проницаемость среды.

Сведем задачу к квадратурам, а также определим число решений, вид их зависимости от параметров и исследуем устойчивость*).

Та же краевая задача получается при определении равновесия в поле искривленного цилиндра в отсутствии нагрузки, если h{x) = hox{l - - x)hi/P, где hi сравнимо с До (в этом случае магнит имеет форму параболического цилиндра).

Решение краевой задачи (6.5.1) суш,ественно зависит от знака 7. Пусть 7 gt; О (нагрузка направлена к магниту). Уравнение в (6.5.1) при этом не имеет особых точек, а его первый интеграл будет

w = 2{vm - v)[{l - Vm)-\l - v)- +7], w = V. (6.5.2)

Здесь Vjn - значение v в точке пересечения фазовой траектории с осью V. Решению задачи (6.5.1) отвечает тот из отрезков АВ фазовых траекторий (рис. 6.11, а), который изображаюш,ая точка пробегает за laquo;время raquo; т = а. Так как линии АВ симметричны относительно Ov, то и форма струны будет симметричной относительно оси, проходяш,ей через ее середину. Величина Vm равна максимальному безразмерному перемеш,ению, достигаемому в середине струны.

(6.5.1)

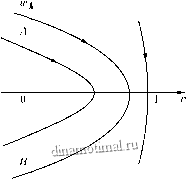
Рис. 6.11, а

[107]

*) Излагаемое ниже решение получено совместно с И.З. Штирельманом

sect;6.5. Равновесие струны

Интегрируя (6.5.2) с учетом условия v{0) =0, получим

- - -1/2

+ 7 ; gt; dz,

г = у lt;J 2{Vm - Z)

]}

(6.5.3)

\ {\-Vm){\-z) О lt; г lt; а/2.

Соотношением (6.5.3) и условием 1;(а -г) = v{t) форма струны определена с точностью до постоянной Vjn, которая найдется из условия - - v{a/2). Тем самым определится зависимость Vm = Vm{oL,). Заменив неременную интегрирования в интеграле, получаюхцемся из (6.5.3) при т = а/2, V = Vjnj приведем его к виду

{1-Z]

п-l/2

L(l -Vm)il -VmZ)

(6.5.4)

Функции r{v) и а{Ут,у) выражаются через комбинации эллиптических интегралов первого и второго рода и элементарных функций. Однако обрагцение этих функций таким путем затруднительно, поэтому будем исходить из выражений с квадратурами.

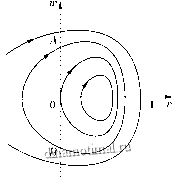
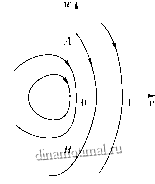
Рис. 6.11, Рис. 6.11, в

Очевидно, что а(0,7) = а(1,7) = О для всех 7 gt; 0. Имеем

да л/2

2 J л/Г о

gi =

[gi {Z, Vm) - g2{z, Vm)g? gt;{z, Vm)],

1-1/2

дз =

1 - m)(l - VmZ] Z - 2VmZ

(6.5.5)

л/(1 - m)(l - VmZ) g2 = л/[1 + 7(1 - m)(l - VmZ)]~.