Динамо-машины  Нелинейная электромеханика 

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 [ 98 ] 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118

Глава 6. Задачи нелинейной теории

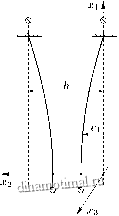
Составим еще уравнения равновесия вертикально подвешенных тяжелых нитей (рис. 6.5).

Ограничимся рассмотрением плоских форм, когда нити располагаются в плоскости Ж1, жз, такие формы, очевидно, заведомо существуют. Как и ранее, имеем Vl = -V2 Положив

2vi/h = V, 1 - V = W,

= = где dg - вес единицы длины нити, получим уравнение

d f dw\ 1 laquo; ..ч

фЫ+г --

с краевыми условиями w{kI) = 1, г(;(0) - ограничено. Уравнение (6.3.11), как и ранее полученное уравнение равновесия ферромагнитной мембраны (6.2.17), представляет собой разно-Рис. 6.5 видность уравнения Эмдена-Фаулера с отрица-

тельной степенью неизвестной функции в нелинейном члене, подробный анализ которого будет сделан в sect; 6.9.

sect; 6.4. Равновесие унруго-закренленных твердых тел

Определим равновесие упруго закрепленного твердого ферромагнитного тела, притягиваемого электромагнитом (рис. 6.6).

Предположим, что тело может смещаться только поступательно, а оба зазора между телом и полюсами магнита одинаковы. Обозначим величину зазоров через h - и, где и - перемещение, h - зазор при недеформированных пружинах. Сила Q, действующая на тело, определится интегрированием выражения (6.2.13) по поверхности полюсов; как полюсы электромагнита, так и примыкающую к ним поверхность тела считаем плоскими. В результате получим известную формулу Максвелла для силы притяжения электромагнита

4{h-u)

(6.4.1)

где I = ni - полный ток (или магнитодвижущая сила обмотки), п - число витков, i - сила тока, S - площадь полюса. Уравнение равновесия будет

си =

4{h-u)

где с - суммарная жесткость пружин.

(6.4.2)

}6.4. Равновесие твердых тел

Введя безразмерные величины V = u/h,

2 PoPS

придем к уравнению третьей степени относительно v с одним параметром а

laquo;2

-(ТЗ- (6-4.3)

Физический смысл имеют только решения г lt; 1. Построив кривую v{a) (рис. 6.7), называемую кривой равновесия, найдем, что нри одном значении параметра система может иметь либо два положения равновесия, либо одно в предельной точке, либо не иметь равновесия вообш,е. Примечательно, что суш,ествует линейная серия положений равновесия (верхняя ветвь), стремяш,аяся при а О не к недеформированному состоянию, а к положению, когда тело и магнит соприкасаются.

Рис. б.б

Рис. 6.7

Следуя результатам sect; 1.2 при исследовании устойчивости, ток в обмотке можно считать независимым параметром и воспользоваться результатами Пуанкаре о смене устойчивости на кривых равновесия.

Система, описываемая уравнением (6.4.3), имеет силовую функцию

2 1-V

(6.4.4)

где П и - соответственно безразмерные потенциальная энергия и энергия магнитного поля. Равновесие будет устойчивым, если при v = = Vr, где Vr - корень уравнения (6.4.3), cPV/dv gt; 0. Возьмем решение V = О при а = 0. Для него dV/dv = 1. Следовательно, это решение устойчиво (что, впрочем, очевидно, так как оно соответствует неде-

Глава 6. Задачи нелинейной теории

формированному состоянию в отсутствии ноля). Отсюда выводим, что устойчива вся линейная серия равновесий от а = О, = О до предельной точки. В предельной точке устойчивость исчезает; верхняя ветвь неустойчива.

Таким образом, в рассмотренной системе возможны лишь пере-меш,ения, составляюш,ие не более одной трети первоначального зазора h (рис. 6.7). Допустимые значения параметра а также ограничены {а lt; 2л/3/9).

При увеличении параметра далее предельного значения равновесие становится невозможным. Это означает, что упруго закрепленное тело laquo;срывается raquo; и ударяется о магнит.

Уравнение (6.4.3) описывает также равновесие тела, поворачива-юш,егося относительно оси согласно рис. 6.8. Обозначим через i9 угол поворота, а через 6 -ширину тела (размер в направлении оси враш,е-пня).

Рис. 6.8

1/2

\\\\\\\

Рис. 6.9

Момент пондеромоторных сил относительно оси равен

М = I xbqdx = fioIb\n{l + l/h)j, (6.4.5)

1 Р

Положив V = а = -fiob--- 1п(1 + l/h), (6.4.6)

А cap

придем к (6.4.3).

Рассмотрим теперь систему, когда ось враш,ения проходит через середину тела (рис. 6.9). Момент пондеромоторных сил на этот раз