 |
www.chms.ru - вывоз мусора в Балашихе |
 |
www.chms.ru - вывоз мусора в Балашихе |
Динамо-машины Нелинейная электромеханика
1 2 3 4 5 6 7 8 9 10 11 12 13 14 [ 15 ] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118
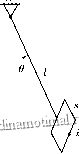
Маятник в переменном магнитном поле
Считая, что частота магнитного ноля много больше собственной частоты колебаний маятника к = г/, введем малый параметр
= . Переходя в уравнениях (1.6.2) к безразмерному (быстрому) времени г = ut и безразмерному току = г/г где базисное значение тока г* = j получим следуюш,ие уравнения в безразмерных переменных:
в - sin т cos в iu- sin 6 gt; = О,
+ sin г cos 6 gt; l9 + cos г sin 6 gt; + Ни = 0.
(1.6.3)
В этих уравнениях введены безразмерные параметры 7 = и г = . В даль-
нейшем сохраним за безразмерными переменными прежние обозначения. Пмея в виду исследование медленных движений, близких к свободным колебаниям маятника, перепишем систему (1.6.3) как
cJ = S7 sin г cos 6 gt; г - г sin в,
к к к
г + sin г COS
+ cos г sin i
Рис. 1.3
+ ri = 0.
(1.6.4)
Система (1.6.4) - квазилинейная с одной некритической быстрой переменной. Как было показано в sect; 1.5, первое приближение асимптотической процедуры описывает консервативную систему. Электромагнитные силы в первом приближении имеют потенциал - среднюю энергию вихревых токов, вычисленных в том же приближении. Консервативность может быть нарушена во втором приближении к электромагнитным силам. При этом, как показано в sect; 1.5, если частота поля превышает величину обратную постоянной времени проводяш,его контура V gt; R/L, то второе приближение электромагнитных сил может носить раскачиваюш,ий характер. Поэтому, не останавливаясь на получении первого приближения, найдем сразу усредненные уравнения медленных движений во втором приближении. Принимая со,в = const, получим второе приближение для тока
8т t
-(sinr + г cost) +1
UJr COS в
((l-r)sinr + 2rcosr). (1.6.5)
1+г2 (1+г2)2
Подставляя это выражение в первые два уравнения системы (1.6.4) и усредняя по быстрому времени г, получим автономное дифференциальное уравнение второго порядка, которое в медленном времени t = kt имеет вид
e-eacose i9 + (cosi9 + 1) sini9 = 0, (1.6.6)
52 Глава 1. Описание электромеханических систем
где а = 2(i7)2 ~ 2(1+г2) Слагаемое (3 cos sin в описывает потепци-альпые электромагнитные силы в первом приближении, а слагаемое -sacos в в - laquo;формально диссипативные raquo; силы, которые в полном соответствии с sect; 1.5 имеют раскачивающий характер при г lt; 1. В дальнейшем будем рассматривать только случай г lt;1, при этом, имея в виду возможность развития автоколебаний, добавим в (1.6.6) чисто диссипативное слагаемое, характеризующее внешнее вязкое трение, в результате чего уравнение медленных колебаний маятника приобретет
в + г{п-а cos в)в + ЦЗ cos i9 + 1) sin i9 = 0. (1.6.7)
В зависимости от величины (3 маятник может иметь либо два, либо четыре положения равновесия. При (3 lt; 1 положения равновесия в = = О, 7г, - нижнее устойчиво, а верхнее неустойчиво. В случае (3 gt; 1 появляются еще два седловых положения равновесия в = 7r=barccos(l/;). При этом в диапазоне параметров п gt; а верхнее и нижнее положение маятника устойчивы, т. е. имеет место эффект стабилизации неустойчивого верхнего положения равновесия за счет действия осциллирующих электромагнитных сил. При п = а устойчивый фокус в положениях равновесия = О, тг переходит в сложный фокус первого порядка. При дальнейшем уменьшении п эти положения равновесия теряют устойчивость с мягким рождением предельных циклов, что означает возникновение в системе автоколебаний с частотой yl -\- (3 около нижнего и с частотой у/1 - (3 около верхнего положения равновесия.
Дальнейшее уменьшение трения приводит к срыву автоколебаний. При этом сперва путем слияния с сепаратрисой, идущей из седла тг - - arccos(l/;) в седло тг + arccos(l/;), разрушается предельный цикл около верхнего положения равновесия, а затем тем же путем при слиянии со laquo;своей raquo; сепаратрисой около нижнего положения. Границы в области параметров, на которых происходит разрушение предельных циклов можно найти, используя метод малого параметра для квазиконсервативной системы (1.6.7). Слиянию предельного цикла с сепаратрисой соответствующей консервативной системы соответствует нуль функции Понтрягина [7]
Ф(/1,(/)1,(/)2) = 2 J{n-a cos в)лУ/З cos2 6 gt; + 2 cos i9 + 2hde, (1.6.8)
где ф1ф2 - координаты седловых точек, соединенные соответствующей сепаратрисой, h = 1/2 - уровень энергии, отвечающий сепара-трисному движению. Таким образом, для определения п = ni{aP) при котором пропадает предельный цикл вокруг в = тг, получим соотношение
Маятник в переменном магнитном поле
(1.6.С
т М 1 1\
W , 7г - arccos -, 7г + arccos - J =
Аналогично находим выражение для определения параметров п = = П2{а,Р), при которых исчезает цикл вокруг = О
Ф,-7г + arccos-,7г - arccos- =0. (1.6.10)
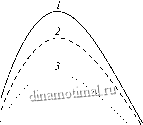
Переходя в соотношениях (1.6.9), (1.6.10) от параметров а, к 7 и г, получим соответствуюгцие неявные зависимости rii (г, 7) и П2 (г, 7). Все бифуркационные кривые п(г) 0,6 при фиксированном 7, (7 = 5) приведе ны на рис. 1.4. Па этом рисунке 1 - граница устойчивости 4 положений равновесия, 2 - граница суш,ествования предельного цикла вокруг в = тг, 3 - граница суш,ествования предельного цикла вокруг 0 = 0.
Кроме медленных колебаний рассматриваемая электромеханическая система допускает также
0,2-
0,2 0,4 0,6
Рис. 1.4
быстрые враш,ательные движения. Пх можно исследовать, сделав в уравнениях (1.6.3) замену переменных гр = О - ftiyt = О - Пт:
ф - sj со8{ф + Пг) sin г г + 8т{ф + Пг) + гп{ф + П) = О, i + cos(0 + Пг) sin t{iI) + П) + sin(0 + Пг) cos г + ri = 0.
(1.6.11)
Здесь в отличие от (1.6.3) уже учтена механическая диссипация. Физически ф задает отклонение траектории движения маятника от врагце-пия с постоянной угловой скоростью rtiy. Полагая скорость изменения гр малой, уравнения (1.6.11) могут быть переписаны в следуюш,ем виде:
ф = ги,
и = s7icos(V + Пг) sinr - S8m{ + Пг) - sn{ip + П), (1.6.12)
i- -\- {ф -\- П) со8{гр + Пг) sin т + 8т{гр + Пг) cos г + ri = 0.
Так же, как и в случае медленных колебаний, система (1.6.12) содержит две медленных переменных и одну некритическую быструю. Используя ту же процедуру, что и ранее, найдем первое приближение для тока:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 [ 15 ] 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 |